The Monty Hall Problem & Other Apparent Paradoxes

[catseye]

Here's another money-based conundrum from today's Quora, with a vaguely similar vibe (BTW, shouldn't the thread be retitled to The Monty Hall and other apparent paradoxes?).

The Rich Guest Paradox

There is a very poor little town where everyone is in a huge debt with someone but with no money to pay for it.
There is hotel which is hardly seeing any business anymore. They are to soon shut it down.
One day a very wealthy American guest shows up and he wants to spend a night there. However before he confirms he asks for a tour of the hotel.
The receptionist asks for a security deposit which the American can take back in case he doesn’t like the rooms. The guest obliges.
It turns out by matter of luck this is the exact amount that the hotel owed to the chef as salary for three months which they hadn’t been able to pay. They gave the cash to the chef.
The chef saw that this was the exact amount of cash he owed the grocer for months of groceries he hadn’t been able to pay for. He paid the grocer.
The grocer realized it was the exact amount he owed the doctor for treating his wife’s arthritis. He paid the doctor.
The doctor paid the money to the nurse for two months of service he couldn’t pay for.
The nurse was new to the town so she had been staying in the hotel for a few days before she found a house to rent. She too was poor and couldn’t pay the hotel at that time. The money she received from the doctor was exactly what she owed the hotel so she paid.
Now the hotel had got back the exact amount it had paid the chef. Now the guest has finished his tour of the rooms. Turns out he doesn’t like it. He takes back his security deposit from the hotel and leaves, never to be seen again.

So everyone's debt has been paid, but nothing is different from before.
No one has earned anything. But now everyone is happy.
Did the debt really exist at all?

PS. I seem to recall something similar to this scenario occurring in a Dads' Army script.

Isn't 'debt', like money, a communal notion? It doesn't really 'exist' in a concrete way - in that anyone could, at any time, decide to just cancel the debt owed to them?

 

[Mikefule]

The Monty Hall problem isn't a paradox, but it is counterintuitive.

The natural intuition, without careful analysis, is if there are 3 doors and 1 car, there "must be" a 1 in 3 chance that the car is behind any door.

In reality, it is 1/3 at the start, but then the situation changes.

The actual case is that Monty Hall never opens the door with the car behind it, so that is giving the contestant some new information. Therefore, the odds change.

The contestant is therefore going from their initial choice, which had a 1/3 chance of being right (based on what was known at that time) to choosing the other remaining door which has a 1/2 chance of being right (based on what is known after the first door is opened).

It took me a long time to get my head round this, but if you do a simple GCSE style "tree diagram" it becomes obvious.

The rich guest paradox is interesting. I had heard a version of this where the porter borrowed the guest's boots, and they were passed all the way round the circle before being left outside the guest's door again. That version did not work quite as well, because the person who put them back was the person who borrowed them.

The version above, with the guest's deposit doing the rounds makes more sense. The bank notes are fungible, and the hotel owner would not know that the money he received was the money he had "borrowed from the deposit".

There is a truth built into the story, that when we live in a society in which debt is the norm, and everyone owns everyone else, it all becomes a shared fiction. It reminds me of all those bank notes that say "I promise to pay the bearer on demand..." which exist solely because no one ever hands one in and says, "I'm the bearer and I'm demanding that you pay me."

 

[Mythopoeika]

It reminds me of all those bank notes that say "I promise to pay the bearer on demand..." which exist solely because no one ever hands one in and says, "I'm the bearer and I'm demanding that you pay me."

I might try that. Aren't the Bank of England required to give me gold?

 

[blessmycottonsocks]

The Monty Hall problem isn't a paradox, but it is counterintuitive.

That's a better description. I suggest the thread be renamed to The Monty Hall problem and other counterintuitive conundrums.

 

[Ringo]

The Monty Hall problem isn't a paradox, but it is counterintuitive.

The natural intuition, without careful analysis, is if there are 3 doors and 1 car, there "must be" a 1 in 3 chance that the car is behind any door.

In reality, it is 1/3 at the start, but then the situation changes.

The actual case is that Monty Hall never opens the door with the car behind it, so that is giving the contestant some new information. Therefore, the odds change.

The contestant is therefore going from their initial choice, which had a 1/3 chance of being right (based on what was known at that time) to choosing the other remaining door which has a 1/2 chance of being right (based on what is known after the first door is opened).

It took me a long time to get my head round this, but if you do a simple GCSE style "tree diagram" it becomes obvious.

I disagree. It is a paradox as the odds change depending upon whether you count an open door as eliminated or not. It is not misunderstood or obvious.

For example, 3 doors each have a 33.3% chance. You choose one. One is opened to reveal nothing. This means there is a 100% chance that it is amongst the other two. Therefore a 50/50 or 1 in 2 chance that you have something behind your door if you count the open door as eliminated.

BUT

3 doors each have a 33.3% chance. You choose one and imagine that you put it in your pocket. That means you have a 33% chance that the prize is in your pocket. But a 66% that it is still on the stage. One of the stage doors is opened. The door hasn't disappeared, it's still there but it is open. There is still a 66% chance that it is on the stage.

It would indeed change to 1/2 chance your door was taken out of your pocket and shuffled randomly with the one remaining closed door. But as it remains in your pocket, the chances that it is behind the closed door on the stage is still 66%.

Or try this, choose a door, put it in your pocket and then open all the doors. The chances that you have the prize is 33%, the chances that it is on the stage is 66%. Opening doors doesn't change the odds but rather your perception of the odds. Hence the paradox.

 

[Mikefule]

I disagree. It is a paradox as the odds change depending upon whether you count an open door as eliminated or not. It is not misunderstood or obvious.

For example, 3 doors each have a 33.3% chance. You choose one. One is opened to reveal nothing. This means there is a 100% chance that it is amongst the other two. Therefore a 50/50 or 1 in 2 chance that you have something behind your door if you count the open door as eliminated.

BUT

3 doors each have a 33.3% chance. You choose one and imagine that you put it in your pocket. That means you have a 33% chance that the prize is in your pocket. But a 66% that it is still on the stage. One of the stage doors is opened. The door hasn't disappeared, it's still there but it is open. There is still a 66% chance that it is on the stage.

It would indeed change to 1/2 chance your door was taken out of your pocket and shuffled randomly with the one remaining closed door. But as it remains in your pocket, the chances that it is behind the closed door on the stage is still 66%.

Or try this, choose a door, put it in your pocket and then open all the doors. The chances that you have the prize is 33%, the chances that it is on the stage is 66%. Opening doors doesn't change the odds but rather your perception of the odds. Hence the paradox.

All we are disagreeing about is the exact definition of the word, "paradox". We have explained the correct answer to the MHP in different terms but without contradiction.

"Paradox" is a much overused word, much like "ironically". Both words are often used when all that is really meant is "surprising".

To me, a paradox is when a series of logical steps appears to contradict itself. The solution to a paradox is to recognise the inherent circular reference and spot the need for a reframing of the terms*. The MHP is a simple probabilities question where most people jump to the wrong conclusion without exploring the simple mathematical steps that show there is only one solution, with no contradiction.

*For example, the Cretan paradox: the Cretan says, "All Cretans are liars." If he's telling the truth then he must be lying.

The Cretan paradox is resolved if the word "liar" is reframed and the Cretan says, "All Cretans lie sometimes." That is, they are still all liars, but they are not lying every time they make a statement.

 

[Rushfan62]

Being given the choice of keeping your door or exchanging it, in effect choosing again from two doors, would give a 50/50 chance of the car. The act of being asked to choose again would trump your original choice. The chance of choosing correctly the first time, is less than the second, but there is no causality between the two, only probability.

 

[Bad Bungle]

I think we're all agreeing on the basic principles of probabilities.

Pick a scenario with two outcomes eg flipping a coin - odds of landing a head is 1/2 (50%), odds of landing a tails is 1/2 (50%). Flip 30 times and you will get (on average) 15 heads and 15 tails. What if you get 5 heads in a row, what are the odds that the next flip will be a tails ? Still 50% overall, the probabilities don't change, they are blind, they don't have a sense of history of what came before.
Pick a scenario with three outcomes eg 3 doors, two goats, one car.
Choose a door, probability/odds of car behind your chosen door is 1/3, odds of car not being behind your door is 2/3
Open all the doors and repeat 30 times - on average you will have picked the car 10 times, a goat 20 times. The odds don't change.
The MHP twist, pick a door and then open one of the other doors (a goat). The odds don't change because the premise hasn't changed, 1/3 the car is behind your door, 2/3 the car is not behind your door.
If one of the other doors contains a goat then the probability the remaining door contains the car is twice as high (2/3) and you should switch doors.

 

[ChasFink]

Being given the choice of keeping your door or exchanging it, in effect choosing again from two doors, would give a 50/50 chance of the car. The act of being asked to choose again would trump your original choice. The chance of choosing correctly the first time, is less than the second, but there is no causality between the two, only probability.

You're missing an important point. After your initial choice, a door was eliminated not by chance, but by deliberate design.

Your initial choice (let's say it was door 1) has a one in three chance of being the car. Nothing can change that - doors can be added to the stage, removed from the stage, a box that may have a helicopter in it may be rolled out. The fact remains that you have a one in three chance of having a car behind your choice.

There is a two in three chance that the car is behind one of the remaining doors. That is, there is a one in three chance it's behind door 2, and a one in three chance it's behind door 3. If you were asked if you want to change your mind at this point, you would neither increase nor decrease your chances.

But Monty does something at this point. He deliberately opens door 2, a door that he knows is not the winner. He then asks if you want to change your mind. You have a one in three chance if you keep the original, but there's a two in three chance that it's behind one of the remaining doors - and you now know you shouldn't pick 2.

 

[IamSundog]

Here's another money-based conundrum from today's Quora, with a vaguely similar vibe (BTW, shouldn't the thread be retitled to The Monty Hall and other apparent paradoxes?).

The Rich Guest Paradox

There is a very poor little town where everyone is in a huge debt with someone but with no money to pay for it.
There is hotel which is hardly seeing any business anymore. They are to soon shut it down.
One day a very wealthy American guest shows up and he wants to spend a night there. However before he confirms he asks for a tour of the hotel.
The receptionist asks for a security deposit which the American can take back in case he doesn’t like the rooms. The guest obliges.
It turns out by matter of luck this is the exact amount that the hotel owed to the chef as salary for three months which they hadn’t been able to pay. They gave the cash to the chef.
The chef saw that this was the exact amount of cash he owed the grocer for months of groceries he hadn’t been able to pay for. He paid the grocer.
The grocer realized it was the exact amount he owed the doctor for treating his wife’s arthritis. He paid the doctor.
The doctor paid the money to the nurse for two months of service he couldn’t pay for.
The nurse was new to the town so she had been staying in the hotel for a few days before she found a house to rent. She too was poor and couldn’t pay the hotel at that time. The money she received from the doctor was exactly what she owed the hotel so she paid.
Now the hotel had got back the exact amount it had paid the chef. Now the guest has finished his tour of the rooms. Turns out he doesn’t like it. He takes back his security deposit from the hotel and leaves, never to be seen again.

So everyone's debt has been paid, but nothing is different from before.
No one has earned anything. But now everyone is happy.
Did the debt really exist at all?

PS. I seem to recall something similar to this scenario occurring in a Dads' Army script.

Everyone’s debt has been paid, but this could have been accomplished without the rich American’s deposit ever being given to the hotel. It’d be the same as saying that I owe you $50 and you owe me $50, so that makes us even.

 

[LymeswoldSnork]

No! Once one door has been opened, you know it's not behind that one, but there is still an equal chance of its being behind either of the others (and having always been there). The only difference is that now there are only two possibilities, so that that equal chance of it being behind whichever door you finally choose is 1 in 2, rather than the 1 in 3 which it was originally. It's just the same as if you started with only two doors.

Can we move onto discussing Carrot In A Box tactics instead?

 

[Ringo]

No! Once one door has been opened, you know it's not behind that one, but there is still an equal chance of its being behind either of the others (and having always been there). The only difference is that now there are only two possibilities, so that that equal chance of it being behind whichever door you finally choose is 1 in 2, rather than the 1 in 3 which it was originally. It's just the same as if you started with only two doors.

Can we move onto discussing Carrot In A Box tactics instead?

Ha-ha! Carrot in a box is too complicated!

However, I beg to differ with your statement above. To prove it, go here: https://www.mathwarehouse.com/monty-hall-simulation-online/
Play 100 times or better still, run the simulation which does it for you but much, much quicker. If you choose "Keep the choice", and your theory is correct then you should win 50% of the time. But you won't. You'll win approx. 33% of the time.

Now do it again and choose "Change the choice". You will win approx. 66% of the time. I just did it. Check out the pic.

 

[SimonBurchell]

I don't get this, it starts as a 3-door problem then turns into a 2-door problem. If you choose once it becomes a 2-door problem, it should be 50-50. Hmmm. My head hurts. Maybe if I reframe it in a Fortean context.

You are out walking alone in the darkened woods when a glowing flying saucer lands in front of you. It has three doors, each with a different symbol. A voice in your head says that behind one of the doors is a wonderful Venusian, but behind the other two are evil little Greys. The voice says you must pick a door. If you get the Venusian, an amazing vision of the future will be revealed to you, if you get a Grey, it's medical examination time. It doesn't matter which door you choose, the telepathic UFO controller, who knows which door the Venusian is behind, will open one of the other doors to reveal a Grey, and asks if you want to change your mind. Does changing your mind help to avoid the evil little goblins?

Nope. Still gives me a headache.

 

[ChasFink]

No! Once one door has been opened, you know it's not behind that one, but there is still an equal chance of its being behind either of the others (and having always been there). The only difference is that now there are only two possibilities, so that that equal chance of it being behind whichever door you finally choose is 1 in 2, rather than the 1 in 3 which it was originally. It's just the same as if you started with only two doors.

Can we move onto discussing Carrot In A Box tactics instead?

And that's where the "paradox" lies. Yes, once a door is shown to be the wrong door, and it will always be a wrong door, there is an equal chance the prize is behind one of the other two. And if someone is asked to make a first choice at that point, it's 50-50, because a door was eliminated before the choice. The game played that way was never a choice among 3 doors, but a choice between 2 doors.

But that wasn't how the problem started. You picked from 3 doors. There's a 1 in 3 chance you were right, and that can't change.

Consider the problem this way: You pick your door. Then the host says "You can trade your door for the best prize behind all the remaining doors - you don't have to choose which one, I'll show you." You then trade your 1 in 3 possibility for a 2 in 3 possibility. He opens the other two doors, each of which has a 1 in 3 possibility, and if the prize is behind either of them you win. This is essentially the same as the original problem, and essentially the same as trading your one original chance for two chances.

Imagine there were a million doors, all closed, and you picked one of them. You have a one in a million chance of picking right with this first choice, and a 999,999 in a million chance of being wrong. Then the host says "You can trade your door for the best prize behind all the remaining doors - you don't have to choose which one, I'll show you." You are now trading your one chance for 999,999 chances.
---------
Edit: I just thought of a much simpler way of proving it, although it won't help anyone actually struggling with the math.

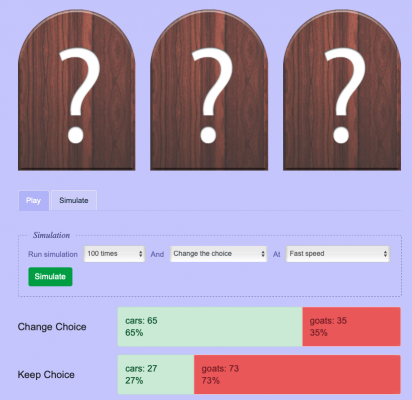
• If you repeated the game over and over, but always stuck with your first choice, how often would you win? The chance of picking right is 1 in 3, so one third of the time.
• If you repeated the game over and over, but always stuck with your first choice, how often would you lose? The chance of picking wrong is 2 in 3, so two thirds of the time.
• If you repeated the game over and over, but always switched, how often would you win? If you picked wrong at first, then you would definitely win by switching, so two thirds of the time.
• If you repeated the game over and over, but always switched, how often would you lose? If you picked right at first, then you would definitely lose by switching, so one third of the time.

 

[blessmycottonsocks]

Quora is quite fertile ground for paradoxes/unintuitive conundrums.
This from today's:

The Potato Paradox.

Let's say you have 100kg of potatoes, which are 99% water by weight.
Now, you leave them outside overnight to dehydrate until they are 98% water.

How much do they weigh now?

Spoiler: Have a guess, then click here...

50 kg!

Here's the maths:

When you had 100kg of potatoes, and water was 99% of the total weight, that meant there were 99kg of water and 1kg of solids.
It's a 1:99 aspect ratio.
Now, when the potatoes dehydrated, causing the water to drop to 98%, solids make up 2% of the weight.

Therefore, the ratio will be 2:98, that is, 1:49. Since solids still weigh 1kg, water must weigh 49kg, which makes a total of 50kg.

 

[TangletwigsDeux]

Head explodes.

 

[Ringo]

Quora is quite fertile ground for paradoxes/unintuitive conundrums.
This from today's:

The Potato Paradox.

Let's say you have 100kg of potatoes, which are 99% water by weight.
Now, you leave them outside overnight to dehydrate until they are 98% water.

How much do they weigh now?

Spoiler: Have a guess, then click here...

50 kg!

Here's the maths:

When you had 100kg of potatoes, and water was 99% of the total weight, that meant there were 99kg of water and 1kg of solids.
It's a 1:99 aspect ratio.
Now, when the potatoes dehydrated, causing the water to drop to 98%, solids make up 2% of the weight.

Therefore, the ratio will be 2:98, that is, 1:49. Since solids still weigh 1kg, water must weigh 49kg, which makes a total of 50kg.

Nope. Ratios are not the same as percentages.

The solids don't gain any weight. They are 1kg and will remain 1kg. The water content will evaporate until (eventually) you're left with only 1kg of bone dry solids.

The ratio of 1:99 isn't percentages. So even if the 1kg of solids now account for 2% of the total weight (or even 20%), the ratio is still 1:98 as in 1kg of solids to 98 kilos of water. So 100kg of potatoes dehydreated to 98% water content will weigh 99kg.

 

[blessmycottonsocks]

It's been well over a year since we had a decent brain exploder here, so how about this very visual jigsaw paradox:

 

[SimonBurchell]

It's been well over a year since we had a decent brain exploder here, so how about this very visual jigsaw paradox:

View attachment 70228

That's making my brain ache looking at it. The only thing I can think is that the diagonal on the two triangles is not at the same angle - they look slightly different on the lower image.

 

[Stormkhan]

Nah. The angle remains the same. Look at the side measurements: in both, the short is 5, middle 13 (You figure out the hypotenuse, Pythagoras!)
It must depend on the shape's dimensions. The orange has moved from above the green (making a rectangle of 5 x 3) to alongside, making a shape 2 x 8.
3 x 5 = 15 and 2 x 8 = 16, 'losing a square' in the difference. Switching the triangles is a neat distraction.

 

[SimonBurchell]

Nah. The angle remains the same. Look at the side measurements: in both, the short is 5, middle 13 (You figure out the hypotenuse, Pythagoras!)
It must depend on the shape's dimensions. The orange has moved from above the green (making a rectangle of 5 x 3) to alongside, making a shape 2 x 8.
3 x 5 = 15 and 2 x 8 = 16, 'losing a square' in the difference. Switching the triangles is a neat distraction.

I'm not so sure - look at the blank space above the diagonals, it doesn't seem to match - I'll bet that's where the blank square is coming from.

 

[Peripart]

That's making my brain ache looking at it. The only thing I can think is that the diagonal on the two triangles is not at the same angle - they look slightly different on the lower image.

That's the key. What looks like the hypotenuse of the overall shape is not in fact a straight line. It dips slightly toward the middle, because the red and green triangles are not similar (in the geometric sense) although they look it.

And the potato thing. The answer really is 50kg, you just need to see that the water diminishes while the solid potato stays at 1kg. Thus if 99% of something is water, and the rest weighs 1kg, it's 100kg in total. If only 98% is water, that's because the 1kg is now 2%, or one fiftieth of the overall. The actual water has evaporated from 99kg to 49kg, a reduction of slightly more than 50% of what it started with.

 

[SimonBurchell]

That's the key. What looks like the hypotenuse of the overall shape is not in fact a straight line. It dips slightly toward the middle, because the red and green triangles are not similar (in the geometric sense) although they look it.

Of course - if the smaller green triangle is 2x5, and the larger red trangle is 3 high (or 1.5x the height of the smaller triangle) then it would have to be 1.5x the width (or 7.5) to maintain the same angle - but the width is actually 8, therefore the angle is different. So some of that white space above the diagonal is engulfed in the shape by shuffling the pieces around.